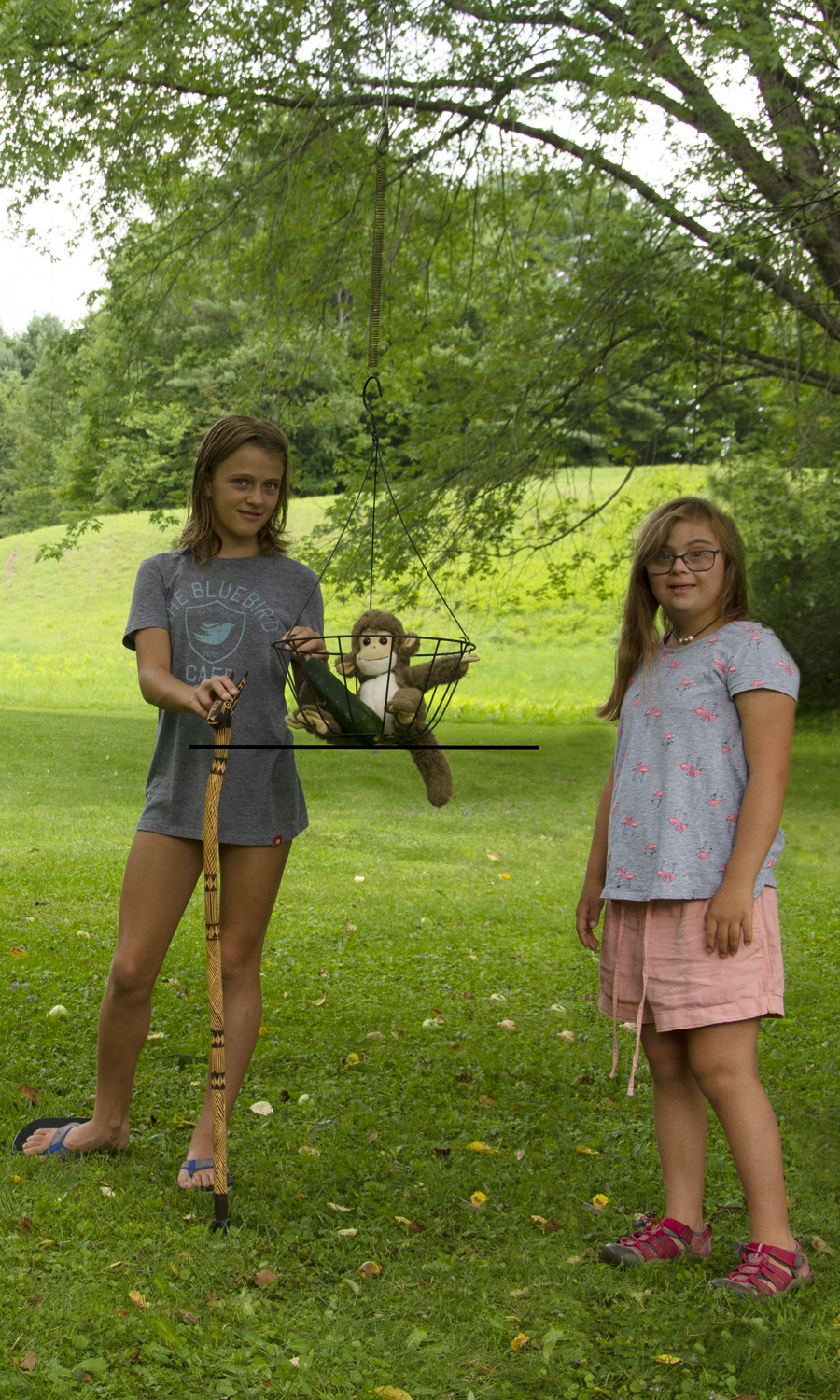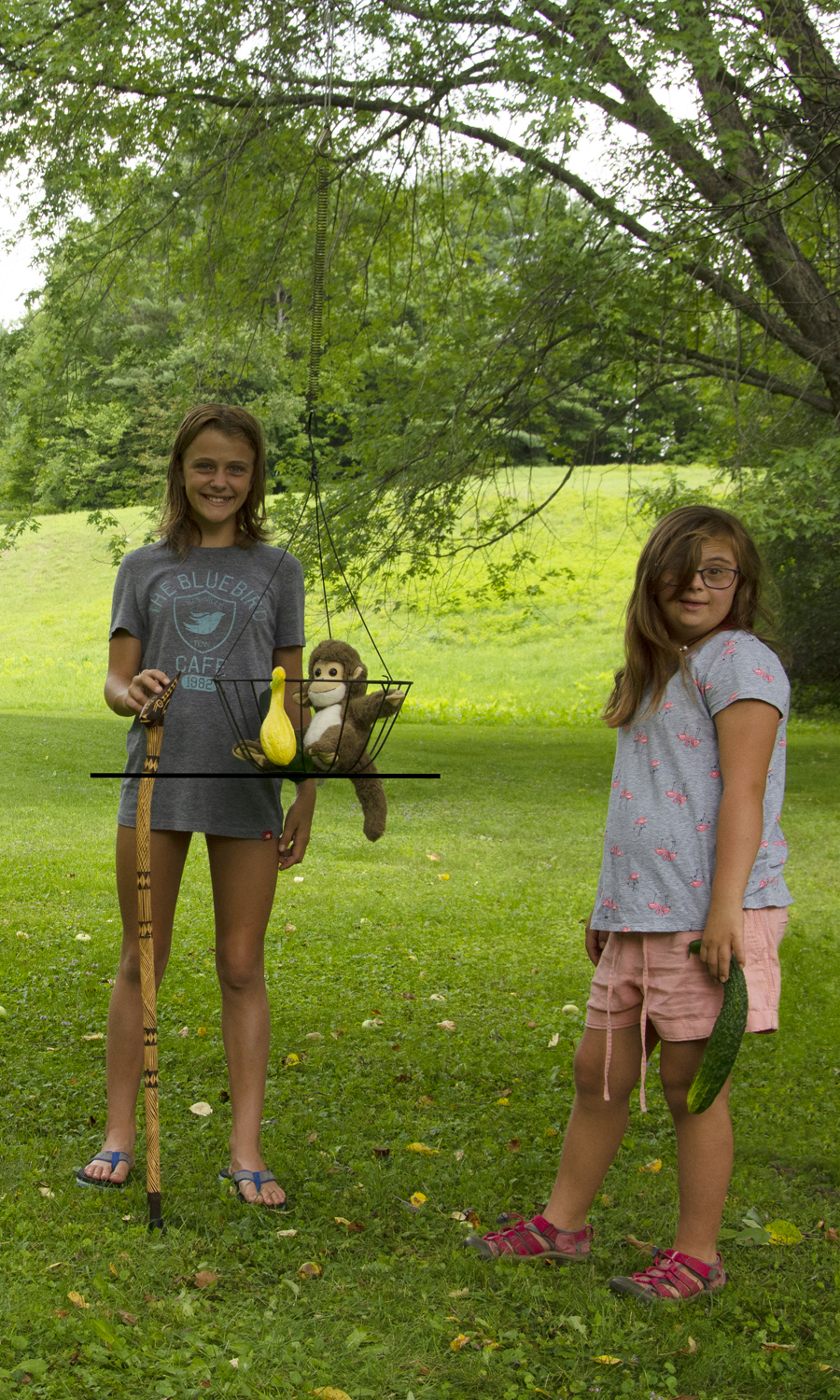Springs
Springs come in many different shapes and sizes.
They are used everywhere. In the store, springs inside scales are used to measure the weight of things from vegetables to nails. In cars, they are used to help make the ride smooth, even on bumpy roads. In sheep pastures, they are used to open and close gates.
What’s so special about springs? To understand, think about a slinky. If you let it sit on a table, it will be unstretched and all closed up. Now suppose you tie one end down and pull on the other end with a ribbon. Remember Newton’s Third Law? It states that for every force, there is an equal and opposite force. When you pull on one end of a slinky, you are exerting a force. The slinky exerts its own force in the opposite direction. That force is called a restoring force, since the slinky is exerting it to try to restore itself to its unstretched length.
If you pull the ribbon a small amount using a small force, the slinky exerts a small force back at you. But if you pull the ribbon a large amount by exerting a large force, the slinky will exert a large force back. Suppose you stretch a slinky between your two hands. When you let go of one side, the slinky will quickly return to its unstretched, closed up shape. This is the restoring force of the slinky at work!
What is true for the slinky is true for springs in general. All stretched springs exert a force to return themselves to their unstretched state. The size of the force depends on just two things: the distance the spring is stretched and the stiffness of the spring. It doesn’t take much effort to stretch a slinky by a few inches, but imagine now much force would be needed to stretch or compress an automobile spring by the same amount!
Hanging Springs
Suppose you hang a stiff spring from a tree and then hang a basket to the bottom. Put something fun in the basket, like a stuffed animal or even a small rock. The spring will stretch by a certain amount. It will stop stretching when the restoring force of the spring (pointing upward) balances the weight of the basket (pointing downward).
Next, hang a floppy spring to the tree and hang the same basket to the end of it. The spring will stretch a lot more before it stops. As with the stiff spring, the floppy spring will stop stretching when its restoring force equals the weight of the basket. But because it isn’t as strong as the stiff spring, it has to stretch a lot more to hold the same weight.
Stiff springs are capable of exerting a larger restoring force than floppy springs. Stiff springs are stronger springs. That’s why you would rather have a stiff, strong spring holding up a car than a floppy, weak one!
If you start hanging more weight onto one of the springs, say the stiff one, it will stretch more with each addition. You can see this by keeping track of where the bottom of the basket is relative to a stick. In the pictures below, the stick shown has an antelope head carved at the top. When only the basket and monkey are hanging, the bottom of the basket is right up near the antelope’s ears at the top of the stick. With an added zucchini, the spring stretches more and the bottom of the basket is below the antelope’s head. When a yellow squash is added, the spring stretches a bit more. And when the cucumber is added, it stretches even more. The extra stretch each time depends on the weight of whatever is added to the basket.
Whenever you hang something from a spring, like a basket filled with stuff, the (upward) restoring force of the spring is equal and opposite the (downward) weight of the basket and the stuff inside. These two forces balance so the net force on the basket and its contents is 0. We know that when there is no net force acting, there is no acceleration. That means that the basket and its contents are either traveling at constant velocity or not moving at all. In the examples shown here, there is no motion. The basket and its contents are sitting still, their weight being balanced by the restoring force of the spring. Whenever a system - which here consists of the basket, its contents and the spring – is not moving because all of the forces cancel each other, we say that the system is in equilibrium.
Bouncing Springs
We will now take a look at a weight bouncing up and down on a spring. Suppose you hang a weight on a spring. It will come to rest - sit still, in other words - at its equilibrium position. In the pictures below, the spring is a slinky and the weight is just a bunch of coils at the end of the slinky, taped together. Let’s call those taped-together coils the “pink disk”. Now suppose you grab hold of the pink disk and pull it down below the equilibrium position.
Pull down on the pink disk below its equilibrium position.
Once you let go, the pink disk starts to bounce up and down between a high point and a low point. This bouncing motion of a weight at the bottom of a spring is called an oscillation and is an example of something called simple harmonic motion. The system, which consists of the spring and the weight at the bottom, is called an oscillator.
After you let go, the pink disk bounces up and back down again, over and over.
There are two ways to explain why this bouncing motion happens. The first way is to consider the forces at work. The second way is to use conservation of energy.
USING FORCE TO EXPLAIN OSCILLATIONS
When you pull down on the pink disk, you need to stretch the spring beyond its equilibrium position. Because the restoring force of the spring increases as it is stretched, that restoring force (pointing upward) is now larger than the weight of the pink disk (pointing downward). The forces don’t balance so there is a net force pointing upward.
There is a net force pointing up when you pull down on the weight at the end of the spring
When you let go of the disk, that net force, pointing upward, causes the disk to accelerate in the upward direction. Its velocity points up too!
When you let go of the disk, it starts to move upward.
When the disk arrives at the equilibrium position, its weight equals the upward restoring force of the spring. The two forces cancel and for this brief moment, the net force is zero and there is no acceleration. But the disk is moving fast in the upward direction. In fact, the disk has its maximum velocity when it passes through the equilibrium position.
When the disk moves through the equilibrium position, it has its maximum velocity. Because the forces are balanced, the net force is zero so there is no acceleration.
As the disk continues to move up, the spring is stretched less and less. As this happens, its restoring force reduces. The downward weight of the pink disk combines with the upward restoring force to make a net force that points downward. This net force causes an acceleration that slows down the disk, since it is in a direction (down) that is opposite the motion (up).
As the disk moves up above the equilibrium position, the net force, and therefore the acceleration, point downward. This causes the disk to slow down because the acceleration is in a direction that is opposite that of the velocity.
The disk slows down until it stops for a brief moment at the top and then starts to travel downward. When it gets to the equilibrium position, the forces once again balance so the net force and acceleration are again both zero, but now the velocity is at its maximum in the downward direction.
When the disk moves through the equilibrium position on the way down, the net force and acceleration are again zero and the velocity is again at its largest value, only now it is in the downward direction.
The disk stops for a moment at the bottom at the same position where you let it go earlier. It then starts moving upward once again. When it stops at the top, it is the same distance above the equilibrium position as it was below the equilibrium position when it stopped there. The motion of the disk repeats over and over again, with the disk moving up and down between a low point and a high point. And it all happens because the restoring force of the spring changes as its length changes, causing an ever-changing net force on the disk.
USING CONSERVATION OF ENERGY TO EXPLAIN OSCILLATIONS
There is an easier way to explain bouncing springs. We can use kinetic and potential energy and the conservation of energy instead. To begin, let’s reconsider what happens when you pull the pink disk down below the equilibrium position. You are applying a force for some distance, so work is being done. In the earlier example of throwing a ball into the air, the work done created some kinetic energy. In this example, the disk isn’t moving when you let go of it, so the work does not create any kinetic energy. Instead, the work goes into the creation of potential energy. We learned about gravitational potential energy earlier. The kind associated with stretching (or compressing) a spring is called spring potential energy. This kind of potential energy increases as the spring is stretched (or compressed) beyond its equilibrium position.
When you pull down on the disk, you apply a force across a distance. The work you do gives potential energy to the spring.
As the disk moves upward after you let go of it, the spring potential energy starts to get converted into kinetic energy. When the disk moves through the equilibrium position, its potential energy is zero. All of the potential energy is now in the form of kinetic energy.
When the disk moves up through the equilibrium position, all of the potential energy is converted to kinetic energy.
As the disk continues to move up, it slows down, so the kinetic energy reduces. As it does, the potential energy increases until the high point, when the disk stops moving for an instant. All of the energy at the upper point is now in the form of potential energy, the same amount that the spring and disk had when the disk was released at the lower point.
When the pink disk stops at the top, it has only potential energy, since the spring is at its most compressed position, and no kinetic energy, since its velocity is zero.
The disk then starts to head back down, through the equilibrium position where the potential energy is once again zero and the kinetic energy is once again maximum.
When the disk moves through the equilibrium position on the way down, its energy is all kinetic once again.
Throughout the up and down bouncing motion, the energy changes from potential to kinetic and back to potential. And the sum of the kinetic and potential energies always stays the same.
One way to illustrate the energy transfer from kinetic to potential and back again is to hang a ball on a spring and take pictures as it bounces up and down. If you look at the pictures side-by-side, you will get a collection of images like the one below.
Pictures of a ball as it bounces up and down on a spring.
The ball starts at the bottom position where the spring is stretched the most. It moves up, through the equilibrium position to the top position where the spring is compressed the most. When the ball is at the very bottom or the very top, it is the farthest from the equilibrium position so it has the maximum potential energy. It has no velocity at these points so it has no kinetic energy; it has only potential energy. When it moves through the equilibrium position - going up or going down - it is moving faster than at any other time during its motion. The potential energy here is zero and the ball has only kinetic energy. The energy switches back and forth between potential and kinetic. As it moves up, it is as if we are pouring energy from the potential energy glass to the kinetic energy glass and then back into the potential energy glass.
The ball has all potential energy at the lowest point in its motion. The potential energy is converted to kinetic energy and then back to potential energy as it moves upward.
As the ball moves down, the energy is once again transferred from potential (at the top) to kinetic (at equilibrium) to potential (at the bottom).
Energy transfers from potential to kinetic and back to potential on the way down, too.
To summarize, an oscillation is a back and forth motion in which the mechanical energy - the kinetic energy plus the potential energy - does not change. The type of energy transfers gradually from kinetic to potential (or from potential to kinetic) during the oscillation, but the sum stays the same. While we can describe this kind of motion using forces, we can also describe it using the conservation of energy. In the next sections we will use the conservation of energy to describe other kinds of oscillations but we will also include short descriptions of the forces at work, too.