Oscillator Basics
The up and down bouncing motion of a weight on a spring is called an oscillation and the spring and weight together are called an oscillator. We have seen that you can describe this back and forth motion using forces or conservation of energy. We will soon see that all back and forth motion works the same way, whether it is bouncing on a spring or swinging on a swing.
No matter what kind of oscillator we are thinking about, there are certain words that apply to all of them. Just as force, velocity, time, mass and acceleration form the basics of the kind of motion we’ve talked about so far, in this section we will learn some new terms that help describe oscillating motion. To get started, consider once again the orange ball bouncing up and down on a spring. The image below, which was introduced in the last section, shows side-by-side pictures of the ball’s changing position as time moves forward, one step at a time.
Pictures of a ball bouncing up and down on a hanging spring. The pictures are taken at 12 evenly-spaced times during the oscillation. The first image is repeated at the end.
In the first frame on the left, the ball is in the lowest position. In successive frames, it moves up to the highest position and then changes direction and moves back down. Earlier, we introduced the term “equilibrium” as the position halfway between the lowest and highest points for an object bouncing on a spring. Equilibrium is the position where the restoring force of the spring is balanced by the weight of the object. In the figure below, a line is drawn through all of the pictures that corresponds to the equilibrium position. The distance between the equilibrium line and the ball at its lowest point is the same as the distance between the equilibrium line and the ball at its highest point. This distance is called the amplitude of the oscillation, and is often described using the capital letter A. The amplitude is the maximum distance (d) the ball (or object) travels above or below the equilibrium position during an oscillation.
The amplitude, A, is the maximum distance from the equilibrium position that the ball reaches when it is bouncing up and down.
Another very important term is used for the time it takes the ball to do one complete oscillation. This time is called the period of the oscillation, and it is often referred to using the capital letter T (since it is a time).
The period, T, is the time it takes for the ball to complete one oscillation.
There are 13 frames shown in the image above. Starting with the first ball on the left, there are 12 steps forward in time to get from one frame to the next until the ball gets back to the same position on the right. If it takes one-tenth of a second (0.1 seconds) to step from one frame to the next, then the period of this particular oscillation is 1.2 seconds (since it takes 12 0.1-second steps to get back to the starting position).
Another term used for one complete oscillation is a cycle. After one cycle, a bouncing (or swinging) object returns to its original position. The term cycle is helpful when people use yet another important term, the frequency of an oscillation. The frequency is a measure of how many cycles can be completed during some amount of time. For this example, the ball completes 1 cycle in 1.2 seconds. With a little arithmetic, we can say that the ball completes 1/1.2 or 0.83 cycles per second. In other words, the ball has a frequency of 0.83 cycles/sec. If the bouncing ball had a period of 2 seconds, its frequency would be 1/2 or 0.5 cycles/sec.
The Period of Oscillation for a Weight on a Spring
Now that we have reviewed the features of a ball (or any object) bouncing up and down on a spring, we might want to know what causes the period of oscillation to be short or long. Imagine a ball that is bouncing very slowly at the end of a spring. If it bounces slowly, its period is long. The velocity of a slowly bouncing ball changes slowly so the acceleration at any point in the cycle must be small. For this to happen, either the restoring force of the spring is small or the mass of the ball is large. (You can use Newton’s Law to arrive at this conclusion.) In other words, when the period is long for an object bouncing on a spring, either the spring is not very stiff (it exerts a weak restoring force) or the mass of the object is large - or both. On the other hand, when the period is short for an object bouncing on a spring, either the spring is stiff (it exerts a strong restoring force) or the mass of the object is small - or both.
Consider a weight, marked with pink tape, bouncing up and down on a weak spring. A camera takes pictures of the bouncing weight every tenth of a second. If cropped images of just the spring and weight are lined up one after the other for one full period, as was done in the illustrations above, the weight can be seen moving down and up as time moves forward. In this example, it takes 8 steps in time for the weight to return to its initial position. Since each time step is one-tenth of a second, the period of the oscillation is eight-tenths of a second (0.8 sec).
A weight bounces on a weak spring; it takes 8 steps in time to complete one period.
Next, the weight with the pink tape is replaced with a lighter (less massive) weight marked with green tape. The same spring is used and the camera once again takes pictures every tenth of a second.
A smaller weight bounces on the same spring shown above. Its mass is less and so is the period of oscillation.
Comparing these two examples, the restoring force of the spring is the same because the same spring is used. From Newton’s Second Law, when the mass is less (with green tape), the acceleration is more than when the mass is greater (with pink tape). A larger acceleration means that the velocity changes more quickly and the time to complete one full oscillation is less. In the series of images, 6 time steps are required to bring the smaller weight back to the starting point, so the period is six-tenths of a second (0.6 sec).
What happens if one of these weights is bounced on a stiffer spring? A stiff spring can exert a larger restoring force than a weak spring. If the same mass, say the heavier one with the pink tape, is bounced on a stiff spring and its motion is compared to when it is bounced on a weak spring, the stiff spring will result in a larger acceleration, a more rapid change in velocity, and a shorter period.
When the large weight is bounced on a stiff spring, its period is shorter than when it is bounced on a weak spring.
Only 4 steps are required to complete one full oscillation when the stiff spring is used. This is a shorter period than we observed when the same weight was bounced on a weak spring. In summary, both the spring stiffness and the mass at the end of the bouncing spring contribute to the period of oscillation. For a given spring, the period is longer when the mass at the end is larger than when it is smaller. For a given mass, the period is longer when the spring is weak than when it is stiff.
The Amplitude of an Oscillator
What about the amplitude of an oscillator? To see if the period depends on the amplitude, consider a carrot bouncing up and down on a slinky with a large and then a small amplitude. As before, the camera takes pictures every tenth of a second and one full period of images are lined up side-by-side.
A carrot bounces up and down on a slinky with a large amplitude (top) and a small amplitude (bottom). The period of oscillation, 10 steps in time, is the same.
In both examples, the bottom of the carrot moves back and forth between a high mark, shown by the blue tape on the pole at left, and a low mark, shown by the green tape. In each case, starting at the top, it takes 10 steps in time for the carrot to return to the top position. Because of friction (for example, air resistance), the amplitude of any object bouncing up and down on a spring decreases slightly as time goes by. We can therefore think of the top (large amplitude) oscillation to have happened at one time and the bottom (small amplitude) oscillation to have happened at a later time. What we see is that as the amplitude decreases, the period of the oscillation stays the same. This important fact is true for all oscillators. The amplitude doesn’t have any effect on the period of oscillation. An object bouncing on a spring will have the same period of oscillation whether the amplitude is big - or small.
Velocity and Acceleration for Oscillators
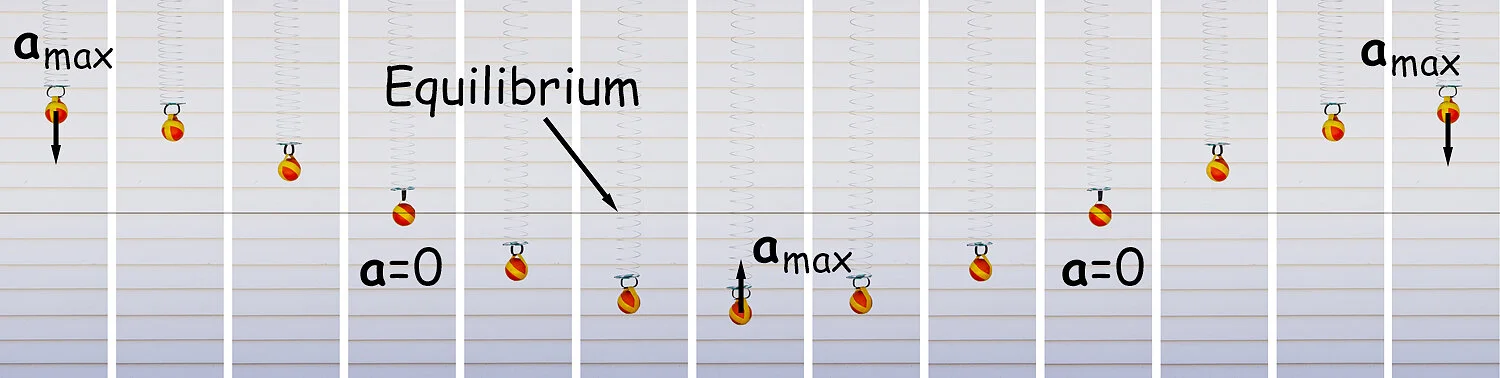
We have learned that the net force on a ball bouncing on a spring changes during an oscillation. This is illustrated below where a series of images, taken at equal time steps, show a colorful ball bouncing on a spring. A line is drawn through all of the images to show the equilibrium position. The force is maximum when the ball is farthest from the equilibrium even though its direction changes, depending on whether it is above or below that point. When the ball is at the equilibrium position, the net force on it is zero.
The net force on a ball changes as the ball oscillates up and down on a spring.
The changing force causes changes in acceleration and velocity as well. Recalling Newton’s Second Law, we know that an object accelerates whenever there is a net force acting on it and it is free to move. This means that the ball has maximum acceleration when the force on it is maximum. That is, the ball has maximum acceleration when it is at its maximum distance from the equilibrium position. The acceleration is zero whenever the ball passes through the equilibrium position.
The ball experiences maximum acceleration when the force is maximum and zero acceleration when the force is zero.
What about the ball’s velocity? Recall that when a ball is thrown straight up into the air, its velocity goes to zero when it is farthest from the ground, at the point where it changes direction and heads back down. The same is true for an oscillator. The velocity is zero when the ball is the farthest away from the equilibrium position. Say the ball is at the upper position. As it heads back toward the equilibrium position, it gains speed. But once it passes through the equilibrium position, it has to start slowing down so that it can stop once again when it gets to the lowest position. It must therefore be going the fastest when it passes through the equilibrium position.
The velocity of the ball is zero when it is farthest from the equilibrium position. The velocity is maximum when it passes through the equilibrium position, moving down or up.
People often get velocity and acceleration confused, but an oscillator is a great example for showing the difference. Acceleration is tied to force. If there is a large force (due to a stretched or compressed spring), there is a large acceleration. That acceleration makes the ball on the end of the spring move, but once it is moving, it passes through a point where there is no longer any force or acceleration (the equilibrium position). It is at that point that the velocity is maximum. In other words, for an oscillator, the velocity is zero when the acceleration is maximum and the velocity is maximum when the acceleration is zero! For any oscillator, we can say that the velocity and acceleration are out of phase with each other. That simply means that whenever one is maximum, the other is not, even though both are changing with the same period (or frequency).